Matematika osmi razreds postopki reševanja in video razlago
Matematika v 8. razredu prinaša pomembne nove pojme in nadgradnjo znanj iz prejšnjih let. Učenci najprej spoznajo množice števil, kot so naravna, cela in racionalna števila. Učijo se unije in preseke množic, ter razumejo njihove odnose. Ob tem utrjujejo računanje v množici naravnih števil in ga razširijo na cela in racionalna števila, kjer spoznajo pojme nasprotnega števila, obratnega števila in absolutne vrednosti.
Sledi poglavje potenc in korenov. Učenci se naučijo pravila za množenje in deljenje potenc z enako osnovo, vrednosti kvadratov naravnih števil do 20, ter kvadratnega korena racionalnih števil. Spoznajo pravilo kvadriranja produkta in kvocienta, koren produkta in količnika, ter se naučijo delnega korenjenja in racionalizacije imenovalca ulomka.
Računanje z izrazi se razširi na enočlenike, dvočlenike in veččlenike. Učenci usvojijo pojem izpostavljanja skupnega faktorja in nadaljujejo z reševanjem enačb in neenačb, kjer razumejo razlike med ekvivalentnimi in identičnimi enačbami.
V zadnjem delu leta se učenci posvetijo geometriji. Spoznajo lomljenke, večkotnike, diagonale in kote večkotnika, ter iz njih izpeljejo pojem pravilnega večkotnika. Naučijo se računati obseg kroga, dolžino krožnega loka, ploščino kroga in ploščino krožnega izseka.
Leto se zaključi z uporabo Pitagorovega izreka v pravokotnem trikotniku in njegovo uporabo v pravokotniku, enakokrakem in enakostraničnem trikotniku ter drugih likih.
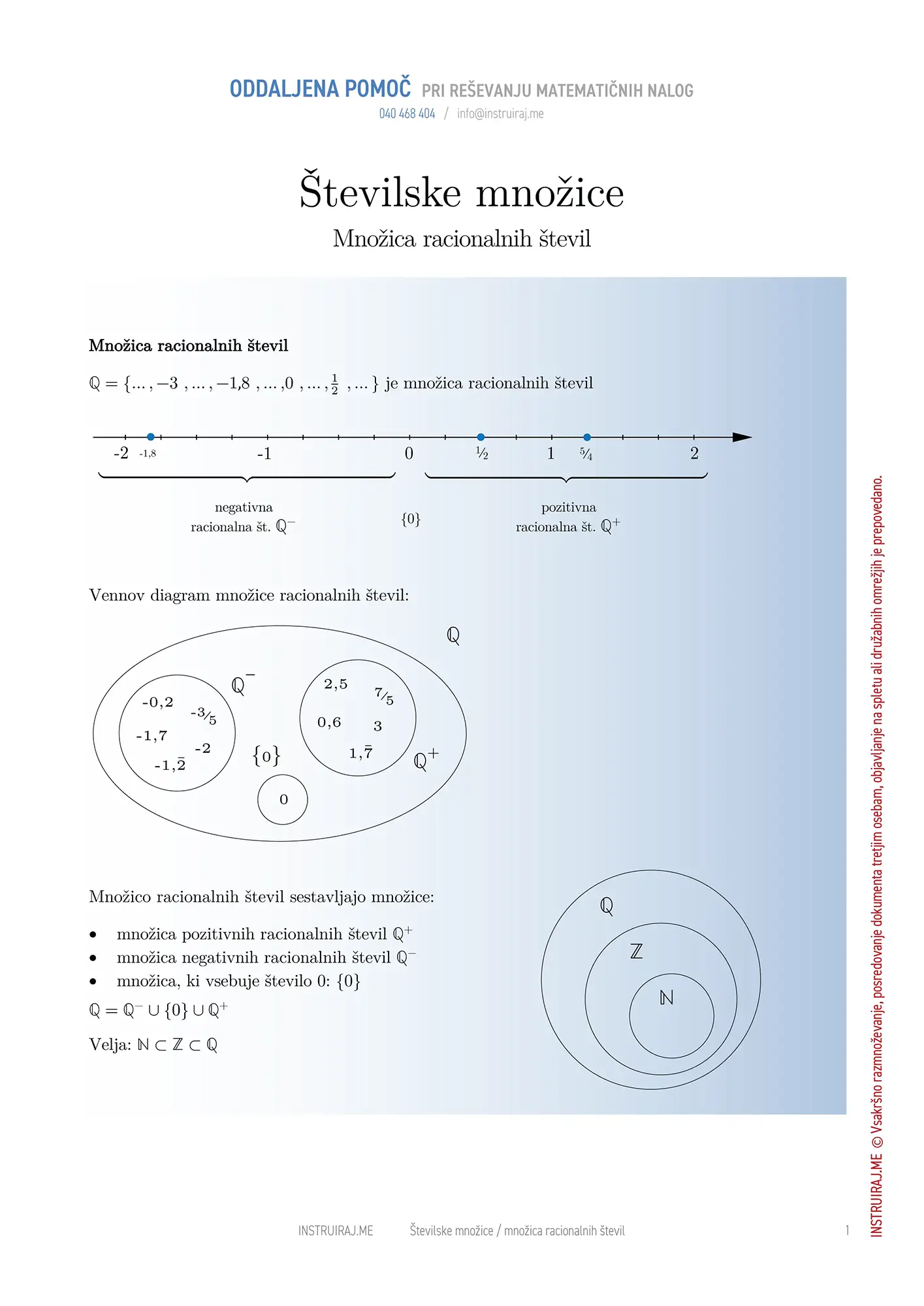
Številske množice
Številske množice so skupine števil z določenimi skupnimi lastnostmi. Naravna števila so tista s katerimi štejemo. Množica celih števil vsebuje vsa naravna števila, njihova nasprotna števila in število 0. Racionalna števila pa so vsa števila, ki jih lahko zapišemo kot ulomek. V to množico spadajo cela števila, decimalna števila in ulomki.
Računanje v množici racionalnih števil
Spoznali bomo postopek, kako se v množici celih in racionalnih števil sešteva in odšteva ter množi in deli. Pozorni bomo morali biti na predznake števil in računsko operacijo.
Potence in koreni
Potence s pozitivnim eksponentom že poznamo, zdj pa bomo spoznali ša potence z negativnim eksponentom. Potenca je sestavljena iz osnove in eksponenta (stopnje) in je uporabna za krajši zapis večjih števil. Spoznali bomo tudi uporabna pravila za računanje s potencami z enakimi osnovami in s potencami z enakimi eksponenti.
Izrazi s spremenljivko
V poglavju Izrazi s spremenljivko bomo spoznali kaj je spremenljivka, kaj je izraz s spremenljivko, in računanje vrednosti izraza. Spoznali bomo kaj je enočlenik, dvočlenik, tričlenik, ... ter kako računamo z enočleniki in veččleniki ter izpostavljamo skupni faktor.
Enačba in neenačba
Enačbe bomo reševali s premislekom, preglednico in diagramom. Preko reševanja enačb pa bomo ugotovili, da so nekatere enačbe ekvivalentne in kaj je identiteta. Poleg enačb bomo reševali tudi neenačbe.
Večkotniki
Večkotniki so lahko izbočeni in udrti ter različnih oblik. Povezali bomo število oglišč večkotnika s številom diagonal, velikostjo notranjih kotov in obnovili znanje o zunanjih kotih.
Krog in deli kroga
Ko spoznavamo krog, moramo razumeti razliko med krožnico in krogom. Ob tem, ko se naučimo računati obseg in ploščino kroga, pa bomo znali računati tudi del krožnice kar imenujemo lok in del kroga, ki mu pravimo krožni izsek.
Pitagorov izrek
Pitagorov izrek govori o povezavi med dolžinami stranic pravokotnega trikotnika. S pomočjo Pitagorovega izreka lahko izračunamo dolžine ene izmed stranic v pravokotnem trikotniku, če poznamo dolžini preostalih dveh stranic. Pravokotne trikotnike bomo našli v različnih likih in s pomočjo Pitagorovega izreka računali dolžine stranic.