Matematični učbenik za osnovno šolospletni učbenik
S strnjeno teorijo, postopki reševanja nalog in video razlago izbranih primerov.
Zbirko matematičnih nalog rešujemo, razlagamo in pregledujemo prof. matematike,
dnevno na voljo za vaša vprašanja in pomoč.
Spoznajmo števila do milijona
Naloge iz poglavja števila do milijona obsegajo razumevanje zapisa samega števila s številko, besedo, desetiškimi enotami, na številski premici ali ga predstavimo s pozicijskim računalom. Iz zapisa s številko ugotovimo ali je število sodo ali liho, sa je pomembna števka na mestu enic.
Računanje s števili do milijona
Preko računanja s številskimi izrazi ponovimo poštevanko in pravila računanja izrazov. Nato nadgradimo pisno seštevanje in odštevanje z večjimi števili brez prehoda in s prehodom. Pri pisnem množenju množimo z enomestnim številom, dvomestnim številom in tromestnim številom. Naloge se ločijo na množenje brez prehoda in na množenje s prehodom. V poglavju zaključimo s pisnim deljenjem z enomestnim in dvomestnim deliteljem.
Merjenje
Pri poglavju merjenje bomo spoznali kako pretvarjati dolžinske enote, denarne enote, enote za merjenje časa in mase ter enote za prostornino. Poudarek bo na pretvarjanju enot in njihovi uporabi.
Deli celote in ulomki
Ulomek je število, ki ga uporabljamo za zapis dela celote. Sestavljen je iz imenovalca, števca in ulomkove črte. V tem poglavju se bomo naučili zapisovati ulomke in jih primerjati med seboj. Opazovali bomo kaj je en del celote in več delov celote, ter se naučili kako z deli celote računati. Pri koncu poglavja pa bomo razumevanje ulomkov povezali s seštevanjem in odštevanjem ulomkov.
Številski in neštevilski izrazi
Matematični zapis s črkami ali številkami imenujemo izraz. Številski izrazi so števila, ki so med seboj povezana s smiselnimi računskimi operacijami. Izrazi s spremenljivkami pa vsebujejo še črkovne oznake.
Množica naravnih števil
Naravna števila so števila, s katerimi štejemo. V tem poglavju bomo ponovili računanje z naravnimi števili, naravna števila bomo urejali po velikosti, ponovili pojem sodega in lihega naravnega števila ter utrjevali prehodnike in naslednike naravnih števil. Spoznali bomo nove izraze velikih naravnih števil, kot so milijarda, bilijon in trilijon ter jih zaokroževali. V množici naravnih števil spoznamo pojma večkratniki in delitelji števil, s pomočjo pravil (kriterijev) deljivosti pa lahko hitro ugotovimo, s katerim številom je določeno število deljivo. Nenazadnje je snov potence za učence zelo zanimiva, saj spoznajo novo računsko operacijo potenciranje in lastnosti potenc, ki dajejo novo možnosti raziskovanja v matematiki.
Izrazi, enačbe in neenačbe
Matematični zapis s črkami ali številkami imenujemo izraz. Poznamo številske izraze, ki so sestavljeni iz števil in računskih operacij, ter izraze s spremenljivkami, ki poleg števil in računskih operacij vsebujejo tudi črkovne oznake - spremenljivke.
Ulomki in decimalni zapis
Ulomek je število, ki ga uporabljamo za zapis dela celote in je sestavljen iz števca, ulomkove črte in imenovalca. V poglavju bomo opazovali primerjavo ulomkov s številom 1. Ulomke z istimi in različnimi imenovalci bomo med seboj tudi primerjali. Naučili se bomo predstavljati ulomke s točko na številski premici in z njimi računali dele celote in celoto. Ob globjem spoznavanju ulomkov jih bomo razdelili na desetiške in nedesetiške ulomke ter jih znali zapisati z decimalnim številom. Decimalna števila bomo tudi zaokorževali na desetine, stotine, tisočine ...
Računanje z decimalnimi števili
V poglavju računanje z decimalnimi števili bomo v začetku ta števila pisno seštevali in pisno odštevali. Nato bomo decimalna števila množili in delili z desetiškimi potencami. Pri množenju decimalnih števil si pomagamo s pisnim množenjem, pri čemer premislimo, kaj se zgodi z decimalno vejico. Pri deljenju decimalnih števil bomo deljenec in delitelja pomnožili z isto desetiško potenco, da se znebimo decimalnih vejic in nato delimo dve naravni števili.
Osnovni geometrijski pojmi
V tem poglavju bomo spoznali točko, premico, daljico, poltrak, ravnino in polravninio. Opazovali bomo odnose med njimi. Naučili se bomo simbolni zapis teh odnosov.
Naravna števila
V množici naravnih števil bomo spoznali praštevila in sestavljena števila. Sestavljena števila bomo z razcepom na prafaktorje zapisali kot produkt praštevilskih potenc. Ponovili bomo večkratnike in delitelje števil ter določali navečji skupni delitelj in najmanjši skupni večkratnik dveh števil. Reševali bomo tako računske, kot besedilne naloge z omenjeno vsebino.
Računanje z ulomki
Ulomke lahko med seboj seštevamo in odštevamo ter množimo in delimo. Pri seštevanju in odštevanju moramo biti pozorni, da imajo ulomki enake imenovalce. Če jih nimajo, ulomke razširimo na skupni imenovalec. Pri množenju dveh ulomkov pomnožimo skupaj števca, nato pa skupaj še imenovalca. Dva ulomka pa med seboj delimo tako, da prvemu ulomku pomnožimo nasprotno vrednost drugega ulomka.
Izrazi in enačbe
Matematični zapis s črkami ali številkami imenujemo izraz. Poznamo številske izraze, ki so sestavljeni iz števil in računskih operacij, ter izraze s spremenljivkami, ki poleg števil in računskih operacij vsebujejo tudi črkovne oznake - spremenljivke. Računali bomo tudi vrednost izraza s spremenljivko in reševali enačbe.
Odstotki
Ulomek je število, ki ga uporabljamo za zapis dela celote. V tem poglavju bomo spoznali, kako delež celote zapišemo z odstotkom. Z odstotki bomo tudi računali s pomočjo ulomkov, sklepanja (preglednice) ali s križnim računom. Predvsem bomo utrjevali snov s pomočjo besedilnih nalog z odstotki.
Transformacije ravnine
Poleg osnov usmerjenosti premice in orientacije likov, bomo spoznali še veliko različnih transformacij ravnine. Spoznali bomo vzporedne premike točke, daljice, premice, lika, ... v ravnini, njihovo zrcaljenje čez premico in točko ter vretenje okoli točke.
Trikotniki
Poznamo različne trikotnike - enakostranične, enakokrake, pravokotne in tiste, ki nimajo posebnih lastnosti. V tem poglavju bomo spoznali izraze kot so višina in težišče trikotnika, trikotniku včrtana in očrtana krožnica. Trikotnike so bomo predvsem naučili načrtovati. Pri načrtovanju trikotnikov si bomo pomagali z znanjem risanja simetrale daljice in simetrale kota.
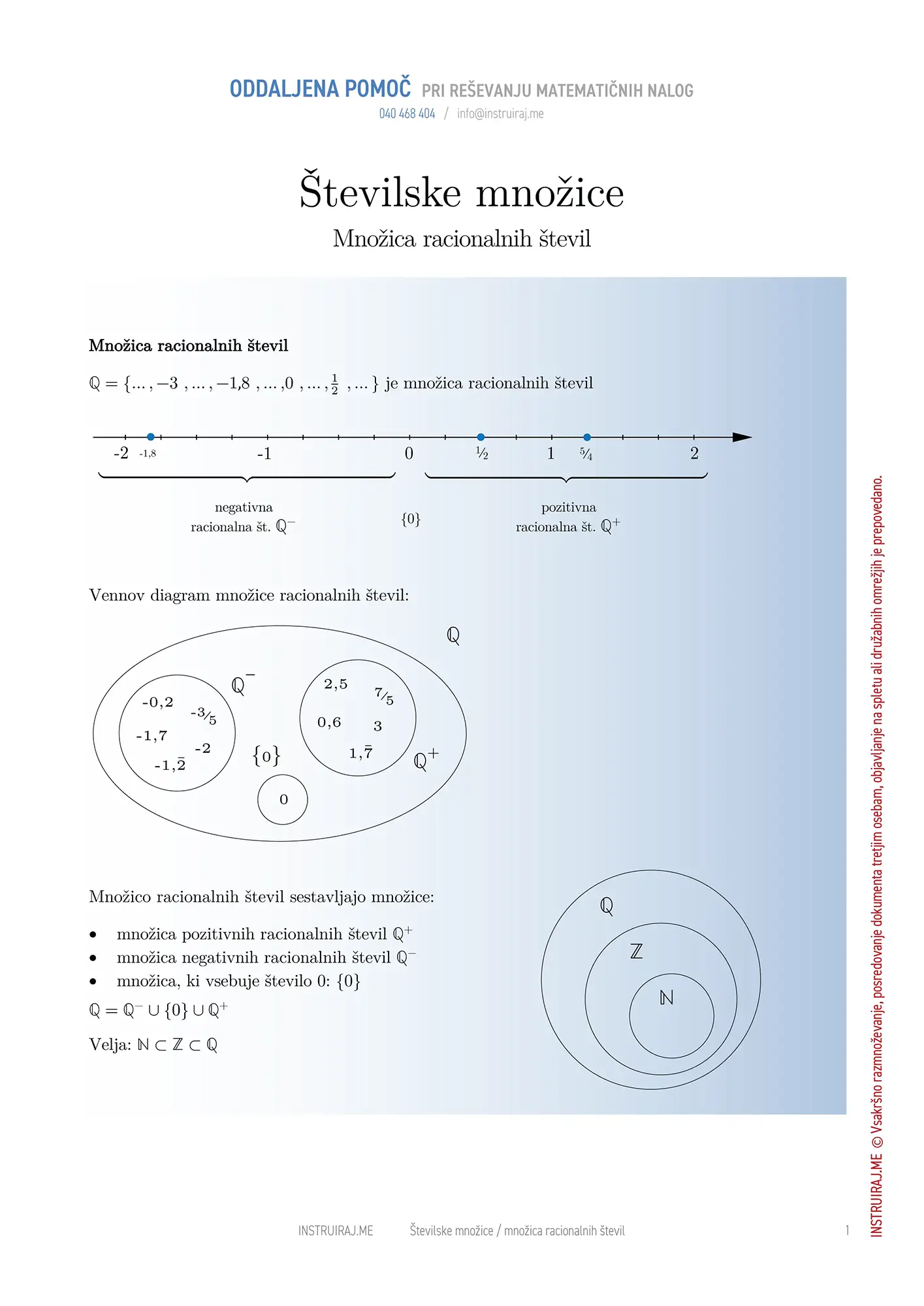
Številske množice
Številske množice so skupine števil z določenimi skupnimi lastnostmi. Naravna števila so tista s katerimi štejemo. Množica celih števil vsebuje vsa naravna števila, njihova nasprotna števila in število 0. Racionalna števila pa so vsa števila, ki jih lahko zapišemo kot ulomek. V to množico spadajo cela števila, decimalna števila in ulomki.
Računanje v množici racionalnih števil
Spoznali bomo postopek, kako se v množici celih in racionalnih števil sešteva in odšteva ter množi in deli. Pozorni bomo morali biti na predznake števil in računsko operacijo.
Potence in koreni
Potence s pozitivnim eksponentom že poznamo, zdj pa bomo spoznali ša potence z negativnim eksponentom. Potenca je sestavljena iz osnove in eksponenta (stopnje) in je uporabna za krajši zapis večjih števil. Spoznali bomo tudi uporabna pravila za računanje s potencami z enakimi osnovami in s potencami z enakimi eksponenti.
Izrazi s spremenljivko
V poglavju Izrazi s spremenljivko bomo spoznali kaj je spremenljivka, kaj je izraz s spremenljivko, in računanje vrednosti izraza. Spoznali bomo kaj je enočlenik, dvočlenik, tričlenik, ... ter kako računamo z enočleniki in veččleniki ter izpostavljamo skupni faktor.
Enačba in neenačba
Enačbe bomo reševali s premislekom, preglednico in diagramom. Preko reševanja enačb pa bomo ugotovili, da so nekatere enačbe ekvivalentne in kaj je identiteta. Poleg enačb bomo reševali tudi neenačbe.
Večkotniki
Večkotniki so lahko izbočeni in udrti ter različnih oblik. Povezali bomo število oglišč večkotnika s številom diagonal, velikostjo notranjih kotov in obnovili znanje o zunanjih kotih.
Krog in deli kroga
Ko spoznavamo krog, moramo razumeti razliko med krožnico in krogom. Ob tem, ko se naučimo računati obseg in ploščino kroga, pa bomo znali računati tudi del krožnice kar imenujemo lok in del kroga, ki mu pravimo krožni izsek.
Pitagorov izrek
Pitagorov izrek govori o povezavi med dolžinami stranic pravokotnega trikotnika. S pomočjo Pitagorovega izreka lahko izračunamo dolžine ene izmed stranic v pravokotnem trikotniku, če poznamo dolžini preostalih dveh stranic. Pravokotne trikotnike bomo našli v različnih likih in s pomočjo Pitagorovega izreka računali dolžine stranic.
Izrazi
Poznamo številske izraze in izraze s spremenljivko. V nadaljevanju se bomo naučili množiti veččlenike in kvadrirati dvočlenike. Spoznali pa bomo tudi razstavljanje, ko izraz zapišemo v obliki produkta.
Enačbe in neenačbe
Enačbe se med seboj razlikujejo po številu neznank in stopnji neznanke. Ko rešujemo enačbo, nas zanima vrednost dane neznanke. To je število, ki reši enačbo (v tem primeru je leva stran enačbe enaka desni). Enačbe lahko rešujemo s premislekom, s preglednico, z diagramom ali s preoblikovanjem.
Sorazmerje in podobnost
Spoznali bomo enakost razmerij, ter ugotovili kdaj sta količini premo ali obratno sorazmerni. S pomočjo razmerij bomo odkrivali tudi podobnost med trikotniki.
Linearna funkcija
Linearna funkcija je ena izmed osnovnih in najpomembnejših funkcij. Spoznali bomo smerni koeficient in začetno vrednost ter ničlo funkcije. Graf linearne funkcije je premica, ki je natanko določena z dvema različnima točkama, ki ležita na njej. Glede na velikost smernega koeficienta bomo ugotovili, kdaj je premica naraščajoča in kdaj padajoča.
Oglata telesa
Že iz prvega razreda osnovne šole se pojavljajo izrazi kocka, kvader, valj, stožec, krogla... Ob spoznavanju tega poglavja pa učenci ne ponovijo le izrazov, temveč računajo površine in prostornine ter ploskovne in telesne diagonale. Pri nalogah se srečajo s preprostimi in težjimi primeri.
Okrogla telesa
Okrogla geometrijska telesa so tista, kjer je vsaj ena ploskev telesa kriva. Mednje prištevamo valj, stožec in kroglo.
Obdelava podatkov
Številna množica podatkov je vir informacij le, če jih znamo razporediti v skupine, iz njih razbrati določene lastnosti in jih pravilno interpretirati. Podatke lahko tudi prikažemo v tabelah, s škatlo z brki ali z različnimi diagrami.
Nacionalno preverjanje znanja
Priprava na NPZ matematika za 9. razred – preveri razlage, postopke in video vsebine od leta 2012 naprej. Poudarek na ključni snovi osnovne šole in točkovanju za vpis v srednjo šolo.